Descarga: sudokusolver.zip.

El siguiente código de alrededor de 150 líneas es un simple solucionador del juego Sudoku escrito en Python 3. Basándose en las reglas del juego, el pequeño programa determina un conjunto de números posibles para cada uno de los casilleros vacíos, y luego aplica fuerza bruta (seleccionar números aleatoriamente hasta obtener el resultado correcto). La fuerza bruta es sin duda uno de los métodos más simples para resolver este tipo de juegos matemáticos, pero no por eso poco eficaz. No será un complejo modelo de Machine Learning pero ha logrado pasar todas las pruebas: desde las grillas más simples a las más avanzadas. El tiempo de resolución del script es generalmente de unos pocos segundos.

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from random import choice


def number_in_row(grid, row, number):
    """
    Chequear si un número se encuentra en la fila especificada.
    """
    return number in grid[row]


def number_in_col(grid, col, number):
    """
    Chequear si un número se encuentra en la columna especificada.
    """
    return number in (row[col] for row in grid)


def number_in_box(grid, row, col, number):
    """
    Chequear si un número se encuentra en la caja a la que
    corresponde la posición especificada.
    """
    # Obtener la caja a la que pertenece el número.
    box_row, box_col = box_by_pos(row, col)
    # Construir una lista con los números en la caja.
    numbers_in_box = unpack(
        row[box_col*3:box_col*3 + 3]
        for row in grid[box_row*3:box_row*3 + 3]
    )
    return number in numbers_in_box


def reduce(n):
    """
    Reducir la posición 9x9 a 3x3.
    """
    n /= 3
    if n == 0 or n != int(n):
        n += 1
    return int(n)


def box_by_pos(row, col):
    # Trabajar temporalmente con base 1.
    row += 1
    col += 1

    # Obtener base 0 nuevamente.
    return reduce(row) - 1, reduce(col) - 1


def unpack(iterable):
    """
    >>> list(unpack([[1, 2], [3, 4]]))
    [1, 2, 3, 4]
    """
    for item in iterable:
        yield from item


def get_possible_numbers(grid, row, col):
    """
    Retorna números posibles para una determinada posición.
    """
    for number in range(1, 10):
        if (not number_in_row(grid, row, number) and
            not number_in_col(grid, col, number) and
            not number_in_box(grid, row, col, number)):
            yield number


def main():
    while True:
        # Los ceros representan casilleros vacíos.
        grid = [
            [0, 0, 0, 8, 0, 3, 0, 0, 0],
            [0, 1, 0, 9, 0, 0, 7, 0, 8],
            [0, 0, 0, 0, 4, 0, 0, 0, 9],
            [2, 0, 0, 0, 0, 4, 0, 6, 0],
            [4, 0, 7, 0, 0, 0, 9, 0, 5],
            [0, 5, 0, 7, 0, 0, 0, 0, 1],
            [7, 0, 0, 0, 3, 0, 0, 0, 0],
            [3, 0, 6, 0, 0, 8, 0, 7, 0],
            [0, 0, 0, 2, 0, 7, 0, 0, 0],
        ]
        
        s = \
        """\
        +-----------------------+
        | {} {} {} | {} {} {} | {} {} {} |
        | {} {} {} | {} {} {} | {} {} {} |
        | {} {} {} | {} {} {} | {} {} {} |
        +-----------------------+
        | {} {} {} | {} {} {} | {} {} {} |
        | {} {} {} | {} {} {} | {} {} {} |
        | {} {} {} | {} {} {} | {} {} {} |
        +-----------------------+
        | {} {} {} | {} {} {} | {} {} {} |
        | {} {} {} | {} {} {} | {} {} {} |
        | {} {} {} | {} {} {} | {} {} {} |
        +-----------------------+
        """
        
        while True:
            possible_numbers = {
                (row, col): None for row in range(9) for col in range(9)
            }
            
            # Obtener una lista de números posibles para cada una de 
            # las posiciones vacías.
            for row in range(9):
                for col in range(9):
                    number = grid[row][col]
                    if number == 0:
                        options = list(
                            get_possible_numbers(grid, row, col)
                        )
                        if options:
                            possible_numbers[(row, col)] = options
            
            # Remover valores vacíos y ordenar por la cantidad de 
            # posibilidades.
            possible_numbers = sorted(
                (
                    (k, v)
                    for (k, v) in possible_numbers.items()
                    if v is not None
                ),
                key=lambda kv: len(kv[1])
            )
            
            if possible_numbers:
                # Obtener el primer item.
                (row, col), numbers = possible_numbers[0]
                # Fuerza bruta: obtener un número aleatorio de la 
                # lista de posibiilidades hasta que la grilla esté
                # completa.
                grid[row][col] = choice(numbers)
            else:
                break
        
        # Chequear si la fuerza bruta dió resultado: si no hay más 
        # ceros en la grilla entonces el Sudoku está resuelto.
        if 0 not in unpack(grid):
            print(s.format(*(unpack(grid))))
            break


if __name__ == "__main__":
    main()

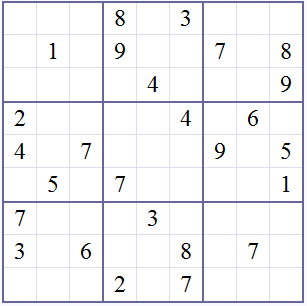
Traté de mantener el código lo más funcional, comentado y legible posible. La grilla por defecto representa el siguiente juego de Sudoku:

Y la solución provista por el programa es:

Para resolver tus propias partidas de Sudoku, simplemente debes editar los elementos de la lista grid.