Versión: 2.x, 3.x
Introducción
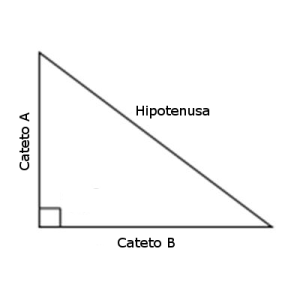
La finalidad de este artículo es desarrollar y explicar paso a paso un pequeño programa que, dados los datos necesarios, resuelva el teorema de Pitágoras. Básicamente lo que éste explica es que la hipotenusa de un triángulo rectángulo al cuadrado es igual a la suma de los dos catetos, ambos al cuadrado. La fórmula sería la siguiente:
Hipotenusa² = Cateto A² + Cateto B²
Basado en esta fórmula, el programa será capaz de aplicar el teorema dados dos valores, calculando el tercero.
Requisitos
Para poder aplicar el teorema no se necesita más que algunas sentencias condicionales y, lo más importante, las funciones para ejecutar la potenciación y radicación. Con respecto a la primera, puede lograrse realizando base**exponente. Por ejemplo:
>>> 5**2 25 >>> 8**2 64
Con respecto a la radicación, utilizaremos la función sqrt del módulo math, que realiza la raíz cuadrada del número indicado:
>>> from math import sqrt >>> sqrt(25) 5.0 >>> sqrt(64) 8.0
Aplicación
Vamos a desarrollar el script paso por paso, los cuales explicaré con detalle. El código se va mostrando de manera ordenada. Al final del artículo puedes encontrar el programa completo.
1
Para comenzar, creamos un nuevo archivo (yo lo he llamado pitagoras.py) y añadimos las siguientes líneas:
#!/usr/bin/env python # -*- coding: utf-8 -*-
La primera para indicarle al sistema cómo interpretar nuestro archivo. La segunda, indica la codificación.
2
Importar la función necesaria para realizar la radicación.
from math import sqrt
3
Queremos que nuestra aplicación corra tanto en Python 2 como en Python 3. En base a los recursos que vamos a utilizar, esto no parece ser un problema. Pero, como debemos solicitar que el usuario ingrese datos vía la entrada estándar, como ya sabrás, la función raw_input ha sido renombrada a input en Python 3. Añadiremos el siguiente código:
try:
input = raw_input
except NameError:
pass
De esta manera aseguramos que en ambas versiones la función input sea la misma. En Python 2 se reemplazará por raw_input. En Python 3, como raw_input ya no se encuentra, será lanzada una excepción del tipo NameError, por lo que se utilizará la función input original.
4
El programa solicitará la entrada de datos numéricos, por lo tanto, necesitamos una función que se encargue de verificar el tipo de cada uno de ellos y, de ser necesario, volver a preguntar.
def get_numeric_value(prompt):
"""
Requests a numeric value from the standard input.
Returns None if no value was inserted.
"""
El parámetro prompt indica la cadena que será pasada a la función input para solicitar la entrada. Es necesario que la función vuelva a preguntar si no se ha indicado un valor numérico. Por último, si no se ha insertado ningún valor, debe retornar None.
while True:
value = input(prompt)
if not value:
return None
try:
value = int(value)
except ValueError:
print("Debe ingresar un valor numerico. "
"Vuelva a intentarlo.")
else:
break
return value
La excepción ValueError será lanzada por la función int al intentar convertir un valor erróneo. Nótese los paréntesis al utilizar print, para mantener la compatibilidad entre las versiones.
5
Requerimos de una función que imprima el dibujo del triángulo rectángulo con sus respectivos valores:
def get_triangle(a=None, b=None, h=None):
"""
Returns a triangle string, with the specified values.
"""
Donde a y b son los catetos y h es la hipotenusa. En donde no se ha especificado un valor, se utilizará el carácter «?»:
return r"""
|\
| \
| \ h
a | \
| \
|_ _ _\
b
a = %s
b = %s
h = %s""" % ("?" if a is None else a,
"?" if b is None else b,
"?" if h is None else h)
La r al comienzo de la cadena es necesaria para que el carácter «\» sea interpretado como tal.
6
Es momento de crear la función principal, la cual se encargará de solicitar los datos, aplicar el teorema e imprimir los resultados. En este paso realizaremos lo primero.
def main():
print(get_triangle())
print("\nDeje en blanco el valor que desconoce.\n")
Esto imprimirá un triángulo en pantalla con todos su valores como incógnitas.
a = get_numeric_value("a: ")
b = get_numeric_value("b: ")
if a is None or b is None:
h = get_numeric_value("h: ")
else:
h = None
A continuación solicitamos los catetos y la hipotenusa (a, b y h respectivamente). A partir de la cuarta línea se verifica si ya se han indicado dos valores; de ser así, no pregunta por el tercero.
if (bool(a) + bool(b) + bool(h)) < 2:
print("Debe especificar, al menos, dos valores.")
return 0
Por último verificamos que se hayan ingresado, al menos, dos valores.
7
Es momento de aplicar el teorema. Antes de eso, hay que determinar cuál es la incógnita.
if h is None:
h = sqrt(a**2 + b**2)
Si el valor desconocido es la hipotenusa, se ejecuta la fórmula tradicional h² = a² + b². Una vez resuelto el término de la derecha, la potencia de la hipotenusa pasa como una raíz que se aplica al primer resultado (a² + b²).
elif a is None:
a = sqrt(h**2 - b**2)
Si es el cateto A o cateto 1, se pasa la suma del cateto B al término izquierdo como una resta, se resuelve, y luego se aplica la raíz proveniente del cateto A, que se encontraba como una potencia en el término derecho.
elif b is None:
b = sqrt(h**2 - a**2)
Por último, si la incógnita es el cateto B, el procedimiento es igual al del cateto A, con la diferencia de que sus lugares se intercambian.
8
Una vez aplicado el teorema, se imprime el resultado en pantalla y finaliza la función:
print("")
print(get_triangle(a, b, h))
return 0
9
Finalmente, el programa sólo debe ejecutarse como un script, llamando a la función principal:
if __name__ == '__main__':
main()
Código completo
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from math import sqrt
try:
input = raw_input
except NameError:
pass
def get_numeric_value(prompt):
"""
Requests a numeric value from the standard input.
Returns None if no value was inserted.
"""
while True:
value = input(prompt)
if not value:
return None
try:
value = int(value)
except ValueError:
print("Debe ingresar un valor numerico. "
"Vuelva a intentarlo.")
else:
break
return value
def get_triangle(a=None, b=None, h=None):
"""
Returns a triangle string, with the specified values.
"""
return r"""
|\
| \
| \ h
a | \
| \
|_ _ _\
b
a = %s
b = %s
h = %s""" % ("?" if a is None else a,
"?" if b is None else b,
"?" if h is None else h)
def main():
print(get_triangle())
print("\nDeje en blanco el valor que desconoce.\n")
a = get_numeric_value("a: ")
b = get_numeric_value("b: ")
if a is None or b is None:
h = get_numeric_value("h: ")
else:
h = None
if (bool(a) + bool(b) + bool(h)) < 2:
print("Debe especificar, al menos, dos valores.")
return 0
if h is None:
h = sqrt(a**2 + b**2)
elif a is None:
a = sqrt(h**2 - b**2)
elif b is None:
b = sqrt(h**2 - a**2)
print("")
print(get_triangle(a, b, h))
return 0
if __name__ == '__main__':
main()
Curso online 👨💻
¡Ya lanzamos el curso oficial de Recursos Python en Udemy!
Un curso moderno para aprender Python desde cero con programación orientada a objetos, SQL y tkinter en 2024.
Consultoría 💡
Ofrecemos servicios profesionales de desarrollo y capacitación en Python a personas y empresas. Consultanos por tu proyecto.

Geronimo says:
estimado: gracias por su enorme contribución, aqui me tome la libertad de agregarle unas lineas para que aparte de los catetos, puedan obtenerse los grados de los triangulos. un fuerte abrazo
Gerónimo
https://mypaste.dev/IkCeUt5W
Recursos Python says:
Hola, Gerónimo. Gracias por tu aporte.
Saludos
Jean Pierre Rodriguez says:
Hola puedes decirme como poner numeros con decimales?
Recursos Python says:
Hola. Deberías reemplazar
value = int(value)porvalue = float(value).Saludos!
Brian says:
Hola, al probar tu codigo en la version 3.7.4 de Python lo ejecuto y me salen algunos problemas de identacion, los corrijo y no imprene ni solicita nada, me gusta tu explicacion porque grafica el teorema
Recursos Python says:
Hola, Podés seleccionar el botón con un «+» para copiar el código con la sangría correspondiente. Saludos.